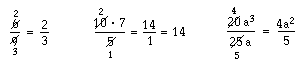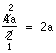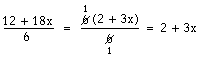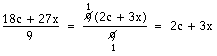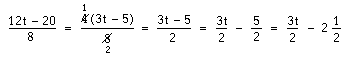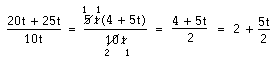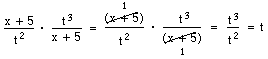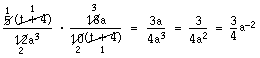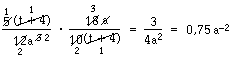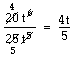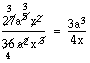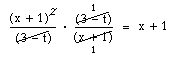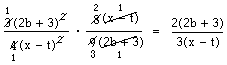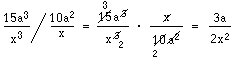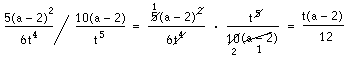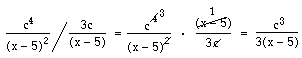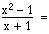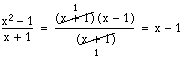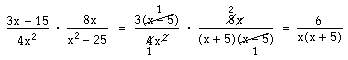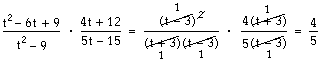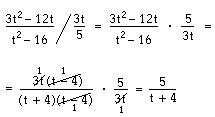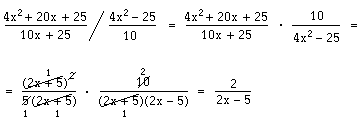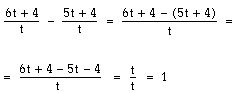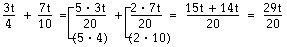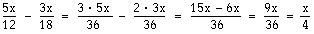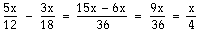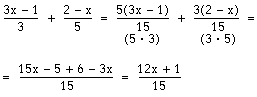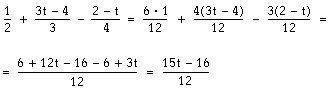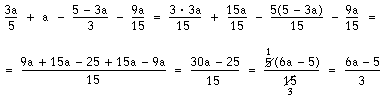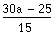Algebra del 9
Förenklingar med faktorisering
Förkortningar är ofta användbart vid förenklingar, både av bråk och av algebraiska uttryck
För att få förkorta måste vi ha faktorer, inte termer. Om vi har
4 + a genom 2, så kan vi inte förkorta mellan fyran och tvåan. Vi har inte två faktorer i täljaren utan två termer.Om vi däremot har 4a genom 2, går det utmärkt att förkorta med två. Du minns ju att 4a betyder 4 · a. Vi har alltså två faktorer i täljaren.
Ett uttryck som 12 + 18x genom 6 kan vi inte heller förkorta. Sexan i nämnaren betyder att hela täljaren, det vill säga de båda termerna 12 och 18x, ska delas med 6. Däremot kan vi bryta ut 6 ur täljaren. Då får vi 6(2 + 3x), och då kommer saken i ett annat läge, för du minns ju att 6(2 + 3x) är samma som 6 · (2 + 3x).
Eftersom täljaren nu består av två faktorer, 6 och (2 + 3x), går det utmärkt att förkorta mellan de två sexorna i täljaren och nämnaren
Du kan komma fram till samma svar genom att först dela 12 med 6 och därefter dela 18x med 6. I det här fallet är väl den metoden snabbare och enklare, men utbrytning är oftast den bästa metoden när uttrycken blir mer komplicerade.
Bryt ut så mycket som möjligt i täljaren. I det senaste exemplet gick det att bryta ut 5t. Det gör att täljaren består av de tre faktorerna 5, t och (4 + 5t). Observera att hela parentesen är en faktor. Det går alltså inte att förkorta mellan femman i parentesen och tian.
Däremot kan du förkorta mellan 10 och faktorn 5 och mellan t:na. Kvar i täljaren får du 1 · 1 · (4 + 5t) = 4 + 5t och i nämnaren 2 · 1 = 2.
Svaren kan oftast skrivas på flera sätt som alla är riktiga. I de två senaste exemplen har vi tre respektive två svar. Vanligast vid denna typ av uppgifter är nog de som står först.
Förkorta bort hela parenteser
Titta på detta exempel:
För att det ska bli lite tydligare har vi satt x + 5 inom parentes både i täljaren och nämnaren. Eftersom parenteserna nu finns som faktorer kan de förkortas bort.
Också i det här exemplet är perenteserna faktorer. Eftersom de är likadana och en står i täljaren och en i nämnaren kan vi förkorta bort dem. Vidare kan vi förkorta 5 och 10 med 5 samt 18 och 12 med 6.
Vi kan dessutom förkorta bort ett a i täljaren mot ett i nämnaren. Detta visar vi genom att ändra exponenten i a
3till en tvåa
Här följer ytterligare några exempel på "exponentförkortning".
Här är det förstås viktigt att du skriver tydligt.
I exemplet ovan betyder ju (x + 1)
2det samma som (x + 1) · (x + 1). En av dessa parenteser kan vi förkorta bort eftersom vi har en likadan parentes i nämnaren. Då återstår bara en parentes (x + 1) i täljaren. Detta markerar vi genom att stryka exponenten 2.
Samma princip går att använda vid division.
Om en faktor består av ett binom som (a – 2), kan man inte förkorta bort en det av binomet. Hela faktorn måste förkortas bort på en gång. Vi kan alltså inte i svaret i exemplet ovan förkorta mellan 2 och 12.
Faktorisering med konjugat- eller kvadreringsregeln
Titta på detta exempel:
Här har vi två termer både i täljaren och nämnaren. Vi kan alltså inte förkorta, trots att det ser frestande ut att stryka bort ettorna och ett x i täljaren och nämnaren. Men täljaren går att faktorisera med hjälp av konjugatregeln. Vi gör ett nytt försök:
Nu kan hela nämnaren förkortas bort mot en motsvarande faktor i täljaren.
Här nedan följer nu några exempel där vi först faktoriserar, antingen genom utbrytning eller genom konjugat- eller kvadreringsregeln. Därefter förkortar vi.
Vi stannar en stund och tittar på det senaste exemplet. Efter faktoriseringen har vi tre parenteser i täljaren; (t + 3) och (t – 3)
2som ju är samma som (t – 3) · (t – 3). I nämnaren har vi också tre parenteser; (t + 3), (t – 3) och (t – 3). Vi kan alltså förkorta bort samtliga parenteser.
Plus och minus med algebraiska uttryck med samma nämnare
Precis som vid bråkräkning gäller att uttryck med samma nämnare direkt kan adderas eller subtraheras.
Plus och minus med algebraiska uttryck med olika nämnare
Även här gäller samma regler som vi bråkräkning. Man måste ta ut minsta gemensamma nämnare (m.g.n.). Du minns väl hur det går till? Om inte får du gå tillbaka till kapitlet om bråkräkning.
Alla uttryck ska ha m.g.n. innan man börjar addera eller subtrahera. Täljarna måste då multipliceras med samma tal som nämnarna multiplicerats med för att få fram m.g.n. Låter det krångligt? Titta här så klarnar det nog:
Minsta gemensamma nämnare är här 20. Vi har multiplicerat den första nämnaren 4 med 5 för att få 20. Alltså multiplicerar vi också täljaren 3t med 5. Den andra nämnaren 10 har vi multiplicerat med 2 för att få 20. Därför har vi även multiplicerat den täljaren 7t med 2. Vi tar ett exempel till:
När du blir säkrare kan du hoppa över mellanledet.
Om täljaren består av ett binom är det viktigt att komma ihåg att hela täljaren ska multipliceras med det tal nämnaren multiplicerats med. För att klart visa detta sätter vi binomet inom parentes.
I nästa exempel ska du notera minustecknet mellan andra och tredje termen. Det ger teckenbyte när du tar bort parentesen på slutet.
Ett sista exempel:
Du ser hur vi gjort för att få a till femtondelar. Vi börjar med att tänka oss a som a genom 1. Sedan multiplicerar vi både täljaren och nämnaren med 15. Du ska alltid sträva efter att förenkla svaret så långt som möjligt.
Du ska inte nöja dig med svaret ovan, eftersom det går att bryta ut 5 i täljaren och sedan förkorta med 5.