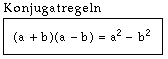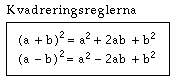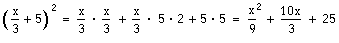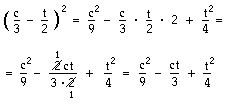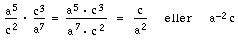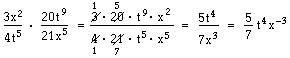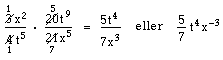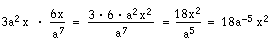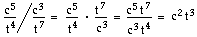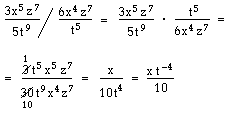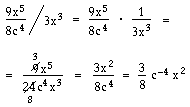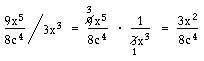Algebra del 7
Konjugatregeln
Tänk att du har två parenteser som ska multipliceras med varandra och som innehåller samma termer, men med olika tecken, till exempel (t + 5)(t – 5) eller (a – t)(a + t). Då finns det en genväg till svaret. För att visa på den genvägen ska vi först utföra de här två multiplikationerna på vanligt sätt:
(t + 5)(t – 5) = t
2– 5t + 5t – 25 = t2– 25(a – t)(a + t) = a
2+ at – at – t2= a2– t2Ser du vad som händer? I det första exemplet tar –5t och +5t ut varandra. Samma sak händer med +at och –at i det andra exemplet. Om parenteserna innehåller samma termer, men med olika tecken tar "mellanprodukterna" alltid ut varandra. Det är konjugatregeln.
I det här speciella fallet, när du har samma termer, men olika tecken, behöver du alltså bara multiplicera de två första termerna och de två andra termerna. Vi tar några exempel till som vanligt:
(x + 4)(x – 4) = x
2– 16(3c + 5)(3c – 5) = 9c
2– 25Som du såg tidigare går det lika bra om minustecknet står i den första parentesen.
(1 – t)(1 + t) = 1 – t
2(3a
5– x3)(3a5+ x3) = 9a10– x6Om ordningen mellan termerna i parenteserna är omkastad, byter man ordningen i den parentes som innehåller plustecknet.
(7 – a)(a + 7) = (7 – a)(7 + a) = 49 – a
2Att vi ändrar ordningen i den parentes som innehåller plustecknet är ganska självklart. Där spelar ju ordningen ingen roll. Det ser du om vi adderar två kända tal, 3 + 2 = 5 och 2 + 3 = 5. Svaret blir detsamma. Så är det inte när det gäller minus, 3 – 2 = 1, men 2 – 3 = –1. Vi tar ett exempel till:
(t + 4)(4 – t) = (4 + t)(4 – t) = 16 – t
2
Kvadreringsreglerna
Ibland händer det att man ska multiplicera två precis likadana parenteser med varandra, som till exempel (a + 5)(a + 5). Det här kan man också skriva (a + 5)2. Vi räknar ut det på vanligt sätt:(a + 5)
2= (a + 5)(a + 5) =
= a2+ 5a + 5a + 25 = a2+ 10a + 25Nu tar vi två exempel till så ska du se att det finns ett mönster.
(3t – 2)
2= (3t – 2)(3t – 2) = 9t2– 6t – 6t + 4 =
= 9t2– 12t + 4(3a + c)
2= (3a + c)(3a + c) = 9a2+3ac + 3ac + c2=
= 9a2+ 6ac + c2Mönstret syns tydligast i svaret före den sista förenklingen. Där får vi den första termen gånger sig själv, två likadana termer och den sista termen gånger sig själv. De två likadana termerna får plustecken om parentesen har plustecken och minustecken om parentesen har minustecken. Den sista termen får alltid plustecken.
Här har vi gjort den sista förenklingen. Man tar den första termen gånger sig själv: a · a = a
2. Därefter tar man den första termen gånger den andra och multiplicerar detta med två: a · b · 2 = 2ab. Tecknet bestäms av tecknet i parentesen. Slutligen tar man den sista termen gånger sig själv: b · b = b2. Vi får alltid plus eftersom både plus gånger plus och minus gånger minus ger plus.Vi tar några exempel till, först på det längre sättet, sedan direkt enligt kvadreringsreglerna.
(c + 9)
2= c · c + c · 9 · 2 + 9 · 9 = c2+ 18c + 81(4t – 5)
2= 4t · 4t – 4t · 5 · 2 + 5 · 5 = 16t2– 40t + 25(t – 1)
2= t2– 2t + 1(7 + 7x)
2= 49 + 98x + 49x2(t
3- 5)2= t6– 10t3+ 25Om parentesen innehåller bråkuttryck kan det bli lite mer komplicerat:
Här kan det vara svårt att använda direktmetoden, speciellt på mellanprodukten. Med lite träning går det naturligtvis, men till en börja kan det vara bäst att räkna ut mellanprodukten separat.
Minustecken eller koefficient framför parentesen
Ibland har man ett minustecken eller en koefficient framför parentesen när konjugat- eller kvadreringsregeln gäller. Då gör man på samma sätt som när ett minustecken eller en koefficient föregår två parenteser som ska multipliceras med varandra.
Man utför alltså först konjugat- eller kvadreringsregeln och låter resultatet stå inom en ny parentes med minustecknet eller koefficienten framför. Därefter skiftar man tecken eller multiplicerar med koefficienten och tar bort parentesen.
–(x + 3)(x – 3) = –(x
2– 9) = –x2+ 9–(5 – b)
2= –(25 – 10b + b2) = –25 + 10b –b25(t –2)(t + 2) = 5(t
2– 4) = 5t2– 203(c + 3t)
2= 3(c2+ 6ct + 9t2) = 3c2+ 18ct + 27t2–4(x
2– x)2= –4(x4– 2x3+ x2) = –4x4+ 8x3– 4x2I den sista parentesen har vi både skiftat tecken och multiplicerat med 4. Mellanprodukten blir x
2· x · 2 = 2x3. Men nu avslutar vi det här avsnittet med ett lite krångligare exempel. Försök att hänga med i svängarna.15x
2– (3x + 4)(3x – 4) – 5(x – 4)2=
= 15x2– (9x2– 16) – 5(x2– 8x + 16) =
= 15x2– 9x2+ 16 – 5x2+ 40x – 80 =
= x2+ 40x – 64
Multiplikation av algebraiska uttryck i rationell form
Vid multiplikation av algebraiska uttryck i rationell form gäller samma regler som vid multiplikation av bråk. Man tar täljarna gånger varandra och nämnarna gånger varandra. Därefter förenklar man om det går.
Förkortningen kan även göras direkt:
Division av algebraiska uttryck i rationell form
Vid division av algebraiska uttryck i rationell form gäller samma regler som vid division av bråk.
Förkortningen kan även göras tidigare:
Faktorisering, utbrytning, konjugatregeln och kvadreringsreglerna baklänges. Till exempel:
6 + 15x = 3 · 2 + 3 · 5x = 3(2 + 5x)
t
2– 9 = (t + 3)(t – 3)